马尔可夫与切比雪夫不等式

最近在学习的时候遇到了一些数学证明，本身并不难，其中用到了马尔可夫不等式，但是不知道没有还是忘了，所以准备借此机会复习一下马尔可夫不等式和切比雪夫不等式（这个肯定学过）。针对这两则定理的证明网上很多很好的博客，包括维基百科，本文虽然是重复造轮子😂，但主要是为了把思考过程记录下来。

马尔可夫不等式

首先把该不等式写下来： $$ P(x>\alpha) <\frac{\mu}{\alpha}, (x>0) $$ 其中x的取值范围为$x>0$，$\mu$为x的数学期望。

看到这个公式，我的第一感觉是这个公式不对吧，公式里连方差都没有，也就是连离散程度都没有涉及怎么能够直接判定其范围呢？我甚至可以直接举出一个“反例”。 试着想象一下：假设x的分布像一条小船，中间概率小，几乎为0，两边大，几乎各占一半。$\alpha$的值比较大，这里假设为10，并且假设在靠近0的地方x的概率密度很大，所以最后的结果是其期望为一个比较小的值，这里假设为1。

之所以认为其是反例的原因是，那么根据马尔可夫不等式，x大于$\alpha$的概率为 $$ P (x>\alpha) <\frac{1}{10} $$ 根据前面所做的设想，这明显“不对”啊，因为值主要分布在两端嘛，怎么可能大于$\alpha$的概率仅为1/10呢？应该是1/2左右吧。

例子如如下图（这里图画的可能不太准确，其实也不可能准确）:

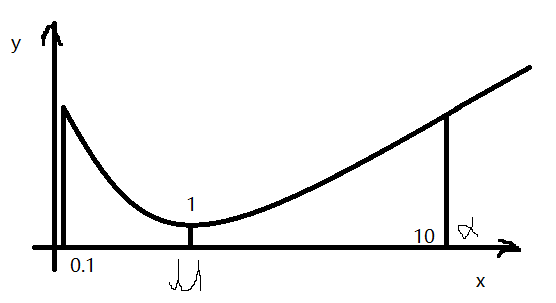
仔细思考后发现该想法是不对的，因为上述想象的图形是画不出来的。假如两边的两个峰值各占一半，那么其期望不可能特别小，其期望的值应该恰好在两个峰值之间，那么马尔可夫不等式的计算结果为1/2，好像符合实际情况😮

再假设其期望就是特别小，比如说1，然后两个峰值相差很大分别为0.1，10。那么根据杠杆原理（乱入😁），期望相当于支点，则两个峰值的数据量之比肯定为10:1。那么根据马尔可夫不等式计算出的值1/10好像又是对的😮。 虽然感觉定理不对，但是为啥举的例子又都是对的呢？后来仔细想想，应该是其条件限制了x的取值范围大于0，期望就相当于支点，距离支点越远，力矩越大，所以需要的力越小，即点的数量也就越少，因此可以得到一个概率范围，嗯~~~听起来挺合理😁

以上只是我一开始的主观想象过程，下面介绍实际的证明： $$ \begin{align} P(x>\alpha) & = \int_\alpha ^\infty f(x)dx \cr & = \frac{1}{\alpha}\int_\alpha^\infty \alpha f(x)dx \cr & < \frac{1}{\alpha}\int_\alpha^\infty xf(x)dx \cr & < \frac{1}{\alpha}\int_0^\infty xf(x)dx \cr & = \frac{\mu}{\alpha} \end{align} $$

其数学证明很简单，值得说明的是该上界经过几次放缩，所以估计的很粗略，相对而言切比雪夫不等式就要准确一些。

切比雪夫不等式

因为切比雪夫中引入了方差，所以感觉看着就比马尔可夫要靠谱些😂 $$ P(|x-\mu |>\alpha) < \frac{\sigma ^2}{\alpha ^2} $$ 其中$\mu$为期望，$\sigma ^2$为方差。

该式的证明也很简单，直接代入马尔可夫不等式就可证明： $$ \begin{align} P(|x-\mu |>\alpha) & = P(|x-\mu |^2>\alpha ^2) \cr & < \frac{E(|x-\mu|^2)}{\alpha ^2} \cr & = \frac{\sigma ^2}{\alpha ^2} \end{align} $$ 上式中的第二步转化之所以成立，是因为$E(|x-\mu|^2)$恰好就是方差的定义啊。可见切比雪夫不等式其实就是对方差的另一种解释。不是方差恰好满足了这个式子，而是方差的定义使其一定满足该不等式。不难想象，如果方差改一下定义，那么切比雪夫不等式肯定以另一种形式出现。

另外，我学的教材中还有对切比雪夫不等式的另一种证明： $$ \begin{align} P(|x-\mu |>\alpha) & = P(|x-\mu |^2>\alpha ^2) \cr & = \int_{|x-\mu |^2>\alpha ^2} f(x)dx \cr & < \int_{|x-\mu |^2>\alpha ^2}\frac{(x-\mu)^2}{\alpha ^2} f(x)dx \cr & < \int_{-\infty}^{\infty}\frac{(x-\mu)^2}{\alpha ^2} f(x)dx \cr & = \frac{\sigma ^2}{\alpha ^2} \end{align} $$

以上为我学的教材上的证明方法，可见切比雪夫不等式中的$|x-\mu|$恰好可以和$f(x)$组成方差的计算公式。通过本博客希望自己对于上述两个不等式有更深的理解吧~😄