主成分分析是一种矩阵的压缩算法,在减少矩阵维数的同时尽可能的保留原矩阵的信息,简单来说就是将 $n×m$的矩阵转换成$n×k$的矩阵,仅保留矩阵中所存在的主要特性,从而可以大大节省空间和数据量。最近课上学到这个知识,感觉很有意思,就在网上找一些博客进行学习,发现网上关于这方面的介绍很多,但是感觉都不太全面,单靠某一个介绍还是无法理解,当然这可能也跟个人基础有关。所以我在这里根据自己的理解写一个总结性的帖子,与大家分享同时也方便自己复习。对于主成分分析,可以参照以下几篇博客:
PCA的数学原理 该博客介绍了主成分中的数学原理,给出了比较清晰的数学解释。简单易懂,但是有一些细节并没有涉及到,所以还是不能完全理解。
PCA 原理:为什么用协方差矩阵 介绍了为什么在降维的时候采用协方差矩阵,但是对于协方差矩阵的解释不详细。
关于协方差矩阵的理解 对协方差矩阵的进行了详细的推导,解释了为什么可以通过$A A^T$来计算协方差矩阵。
矩阵求导、几种重要的矩阵及常用的矩阵求导公式 对矩阵求导进行了介绍。提到了可能会用到的一些求导公式。
UFLDL 教程学习笔记(四)主成分分析 对主成分的原理和使用进行了介绍。
1. 数学原理
数学原理的介绍部分可以参考文献1,该博客对主成分分析的数学原理进行了很直观的介绍。这里我根据自己的理解进行简单介绍。
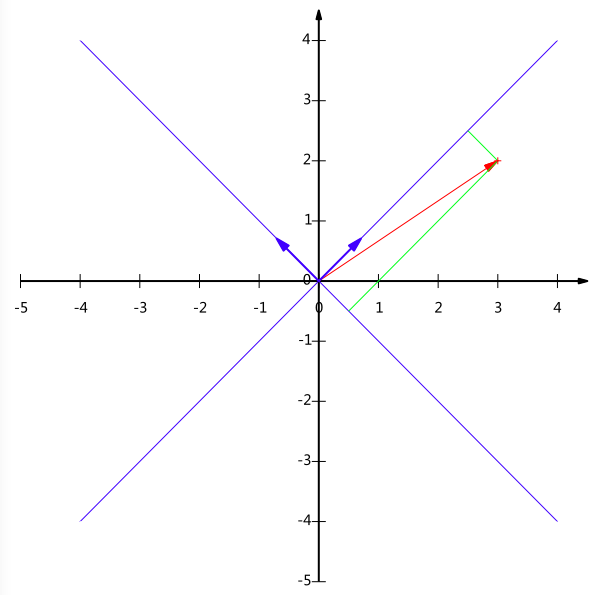
图一(图片来源于文献 1)
对于一个坐标点$(3,2)$,我们知道其代表的意思是在二维坐标里其横坐标为3,纵坐标为2。其实这隐含了一个假设,即其横纵坐标的基为$(1,0)和(0,1)$。对于一般的二维向量,这似乎是大家的默认情况,就像随便给出一个数字$10$,大家会认为这是$10$进制表示,除非特殊标明,不会把它当作其他进制来理解。对于任意一个坐标点$(x,y)$,我们可以将其表示为:
$$
\begin{pmatrix}
1 & 0 \cr
0 & 1
\end{pmatrix} \cdot
\begin{pmatrix}
x \cr
y
\end{pmatrix} =
\begin{pmatrix}
x \cr
y
\end{pmatrix}
$$
其中$\begin{pmatrix}
1 & 0 \cr
0 & 1
\end{pmatrix}$的每一个行向量代表一个基向量。
如果我想更换基向量怎么办呢,如上图所示,如果我想知道$(3,2)$在$(\sqrt{2}/2,\sqrt{2}/2)与(-\sqrt{2}/2,\sqrt{2}/2)$基下的坐标值,该如何计算呢?回顾基本的数学知识,我们发现对于一个向量在一个基上的值其实就是该向量在该基向量上的投影。所以,已知基向量,我们可以很容易求得,对于一个向量,如$(3,2)$,其在基$(\sqrt{2}/2,\sqrt{2}/2)与(-\sqrt{2}/2,\sqrt{2}/2)$上的投影为:
$$
\begin{pmatrix}
\sqrt{2}/2 & \sqrt{2}/2 \cr
-\sqrt{2}/2 & \sqrt{2}/2 \cr
\end{pmatrix} \cdot
\begin{pmatrix}
3 \cr
2
\end{pmatrix} =
\begin{pmatrix}
5\sqrt{2}/2 \cr
-\sqrt{2}/2
\end{pmatrix}
$$
直观的图表示如上图所示。
再回到主成分分析上来,如果我们想对一个矩阵$A$进行降维,其中$A$为:
$$
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \cr
a_{21} & a_{22} & \cdots & a_{2n} \cr
\vdots & \vdots & \ddots & \vdots \cr
a_{m1} & a_{m2} & \cdots & a_{mn} \cr
\end{pmatrix}
$$
行向量代表样本,列向量代表特征,所以其矩阵含义为m个具有n个特征的样本值。对于每一个样本具有的n个特征值,其特征值之间可能会存在很大的耦合,就如文献1中所列举的那样,特征M代表是否为男性,特征F代表是否为女性,因为一个人的性别只能为其中的一个(不考虑特殊情况)。所以这两个特征只留一个就行了,所以就可以省下一半的空间。这个例子有些极端,但是并不影响理解。
图二(图片来源于网络)
同样对于一个具有n个特征的集合来说,很难说这n个特征都是完全有必要的,所以我们就想办法来精简一些特征。选取少于n个的基向量组,将数据投影在这个向量组上,减少空间的同时又能保证信息量。首先需要明确的一点是什么才算好的基向量?首先举一个将二维空间的数据投影到一维空间的情况。如上图所示,对于空间中的这些点,我们应该怎么投影才能够尽可能的保持数据的信息量呢?通过上图中可以看出,如果将数据投影到PC1上,那么所有的数据点较为分散,与之相反,如果投影到PC2上,则数据较为集中。考虑一个极端的情况,假如所有的点在投影之后全部集中在一个点上,这样好吗?当然不!如果所有的点都集中到一个点上,那就说明所有的点都没有差别,信息全部丢失了。所以我们希望当数据点投影到某个坐标轴之上以后,数据越分散越好 ,而衡量一组数据是否发散恰好有一个统计名词“方差”,也就是说投影过后的点值方差越大越好。
同时,如果数据被投影到多个基向量上,那么我们希望这些基向量之间的耦合程度越小越好,也就说基向量之间应该是正交的,如图三所示(建议点击链接去相应网站查看3D演示)。因为如果不考虑基向量之间的正交性,只考虑方差最大的话,那么所求得的所有的基向量其实都是一样的。关于在不同的基向量上的投影的线性相关度也有一个度量标准–协方差。那么我们的目标明确了,使得相同特征之间方差越大越好,不同特征之间协方差越小越好 。
那么这些方差,协方差什么的怎么计算呢?这里可以先给出一个结论,将$A$向量的每一列减去该列的平均值得到一个新的$A$矩阵。然后计算$Cov=1/m \cdot A^T\cdot A$,得到一个$n\times n$的矩阵$Cov$,那么$Cov$的对角线上的元素$c_{ii}$即为第i个特征的方差,对于其他元素$c_{ij}$表示第i个和第j个特征的协方差,很明显该矩阵是对称矩阵。关于该矩阵的计算方式可以参考文献3,其介绍的很详细,这里就不再重复。需要注意的一点是这里$Cov=1/m \cdot A^T\cdot A$是因为A矩阵的列向量为特征,所以才这样计算。如果A矩阵的行列向量所表达的含义相反则$Cov=1/m \cdot A\cdot A^T$。
已经知道了计算协方差矩阵的方法,下面看一下怎么跟我们要做的结合在一起。再次总结一下我们要做的是什么,对于一个已有的矩阵$A$,我们希望将它投影在一组新的基空间上,使之矩阵大小得到压缩。即:
$$
D_{m,N} = A_{mn} \cdot P_{nN}, \ \ \ \ given (N < n)
$$
我们要做的就是将n个特征压缩为N个特征。对于压缩过的数据投影,根据上面的叙述可知,我们希望对于相同特征之间方差越大越好,不同特征之间协方差越小越好 ,并且我们已经知道该如何计算方差和协方差了。
$$
Cov(D)_ {N,N} = D^T \cdot D = P^T A^T A P.
$$
所以现在的目标很明确,我们要做的就是求得$P$,使得$Cov(D)$的对角线元素尽可能大,非对角线元素尽可能小。学过线性代数的应该都知道,对于$A^T A$矩阵来说,其特征向量组就满足这一条件。因为已知$A^T A$矩阵为对称矩阵,所以可知:
$$
P^T (A^T A) P = P^{-1} (A^T A) P = \Lambda
$$
其中$\Lambda$为$A^T A$的特征值组成的对角阵,$P$为相应的的特征向量组。
至此,我们就找到了进行主成分分析的方法:
首先对矩阵A进行处理,使得其每一列(或者行)减去其相应列的平均值,使得每一列的平均值都为0,然后计算$B = A^TA$。
求$B$矩阵的特征值和特征向量,将特征值进行排序,并选取前N大的特征值,选取其对应的特征向量组成特征向量组$P_{nN}$。
$D_{m,N} = A_{mn} \cdot P_{nN}$即为最终想要得到的值。
2.实验验证
下面我们对该算法进行实际的实现,为了更好的了解PCA的工作原理,同时又保证程序的计算速度,我才用了C语言进行实现,并借助OpenBLAS库进行高效的矩阵运算。OpenBLAS 是BLAS标准的一个开源实现,据说也是目前性能和维护的最好的一个。BLAS 是Basic Linear Algebra Subprograms的简称,是一个矩阵运算的接口标准。既然是接口标准,那么所有根据该标准的实现都具有相同的使用方式和功能。相似的实现还有BLAS、MKL、ACML等,我使用OpenBLAS进行实现,因为其实现不依赖于任何平台,具有良好的性能,而且亲测易于安装。下面将附上我的实现代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
//矩阵运算部分 Matrix.cpp
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
//#include "mkl.h"
#include"OpenBLAS/cblas.h"
class Matrix
{
public :
//Print matrix;
bool printMatrix () const ;
//get r.
int getr () { return r ;}
//get l.
int getc () { return c ;}
//get a.
float * geta () { return a ;}
//normalization.
void nmlt ();
//Compute Coevariance of a, aTxa
void coev ( Matrix & c );
//Default constructor.
Matrix () : a ( NULL ), r ( 0 ), c ( 0 ) {}
//Constructor with matrix pointer and dimension.
Matrix ( float * aa , int rr , int cc ) : a ( aa ), r ( rr ), c ( cc ) {}
//Constructor with only dimension, should allocate space.
Matrix ( int rr , int cc ) : r ( rr ), c ( cc )
{
a = new float [ rr * cc ];
}
//Destructor.
~ Matrix () { delete [] a ; a = NULL ;}
protected :
//Matrix pointer.
float * a ;
//Dimension n, order lda
int r , c ;
};
extern bool printArray ( float * p , int n );
class SquareMatrix : public Matrix
{
public :
//Default constructor.
SquareMatrix ( float * aa , int nn ) : Matrix ( aa , nn , nn ), n ( nn ) {}
SquareMatrix ( int nn ) : Matrix ( nn , nn ), n ( nn ){}
//Destructor.
~ SquareMatrix () {}
//Get eigenvalue and eigenvector;
int ssyevd ( float * w );
private :
int n ;
};
bool Matrix :: printMatrix () const
{
int i = 0 , j = 0 ;
float temp ( 0 );
for ( i = 0 ; i < r ; i ++ )
{
for ( j = 0 ; j < c ; j ++ )
{
temp = * ( a + c * i + j );
printf ( "%7.3f \t " , temp );
}
std :: cout << std :: endl ;
}
}
int SquareMatrix :: ssyevd ( float * w )
{
lapack_int res = 0 ;
res = LAPACKE_ssyevd ( LAPACK_ROW_MAJOR , 'V' , 'U' , n , a , n , w );
if ( res == 0 )
{
return res ;
}
else
{
std :: cout << "ERROR:" << res << std :: endl ;
exit ( - 1 );
}
}
void Matrix :: coev ( Matrix & cc )
{
nmlt ();
cblas_sgemm ( CblasRowMajor , CblasTrans , CblasNoTrans , c , c , r , 1.0 / r , a , c , a , c , 0.0 , cc . geta (), c );
}
void Matrix :: nmlt ()
{
int i = 0 , j = 0 ;
float av = 0.0 ;
for ( i = 0 ; i < c ; i ++ )
{
av = 0.0 ;
for ( j = 0 ; j < r ; j ++ )
{
av +=* ( a + i + j * c );
}
av = av / r ;
for ( j = 0 ; j < r ; j ++ )
{
* ( a + i + j * c ) -= av ;
}
}
}
bool printArray ( float * p , int n )
{
for ( int i = 0 ; i < n ; i ++ )
{
printf ( "%7.3f \t " , p [ i ]);
}
std :: cout << std :: endl ;
return true ;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
//PCA部分 PCA.cpp
#include<iostream>
#include<stdio.h>
#include<stdlib.h>
//#include "mkl.h"
#include"OpenBLAS/cblas.h"
#include"Matrix.h"
#include"PCA.h"
#define N 5
#define T 0.8f
const char SEP = ',' ;
static unsigned int R = 5 ;
static unsigned int C = 5 ;
int main ( int argc , char * argv [])
{
// float *A = new float [N*N]
// {
// 1.96f, -6.49f, -0.47f, -7.20f, -0.65f,
// -6.49f, 3.80f, -6.39f, 1.50f, -6.34f,
// -0.47f, -6.39f, 4.17f, -1.51f, 2.67f,
// -7.20f, 1.50f, -1.51f, 5.70f, 1.80f,
// -0.65f, -6.34f, 2.67f, 1.80f, -7.10f
// };
if ( argc <= 1 )
{
printf ( "Usage: PCA [INPUT FILE] [OUTPUT FILE] [ROW] [COLUM] \n " );
printf ( "INPUT FILE: input file path. \n " );
printf ( "OUTPUT FILE: output file path. \n " );
printf ( "ROW: Row of matrix. \n " );
printf ( "COLUM: Colum of matrix. \n " );
exit ( 0 );
}
FILE * input = fopen ( argv [ 1 ], "r" );
FILE * output = fopen ( argv [ 2 ], "w+" );
R = atof ( argv [ 3 ]);
C = atof ( argv [ 4 ]);
printf ( "Input:%s \n Output:%s \n R:%d \n C:%d \n " , argv [ 1 ], argv [ 2 ], R , C );
float * I = new float [ R * C ]();
//float *O = new float[R*C]();
char * label = new char [ R ];
//read matrix.
readMtx ( input , I , label );
SquareMatrix cov = SquareMatrix ( C );
float * eValue = new float [ C ]();
Matrix m = Matrix ( I , R , C );
Matrix n = Matrix ( R , C );
// m.printMatrix();
//compute coveriance matrix.
m . coev ( cov );
//compute eigenvalue and eigenvector of coveriance matrix.
cov . ssyevd ( eValue );
//Compute compressed matrix.
eMtx ( m , cov , n );
//n.printMatrix();
saveMtx ( output , n . geta (), label );
fclose ( input );
fclose ( output );
delete [] label ;
delete [] eValue ;
return 0 ;
}
//eigen matrix
void eMtx ( Matrix & a , Matrix & b , Matrix & r )
{
cblas_sgemm ( CblasRowMajor , CblasNoTrans , CblasNoTrans , a . getr (), b . getc (), a . getc (), 1.0 , a . geta (), a . getc (), b . geta (), b . getc (), 0.0 , r . geta (), b . getc ());
}
bool readUtl ( FILE * f , char sep )
{
char c ;
if (( c = fgetc ( f )) != EOF && c == sep )
{
return true ;
}
return false ;
}
void readMtx ( FILE * f , float * m , char * la )
{
float ft ( 0.0 );
char ch ;
int i ( 0 ), j ( 0 ), index ( 0 );
while ( i < R )
{
while ( ! readUtl ( f , SEP ));
la [ i ++ ] = fgetc ( f );
readUtl ( f , SEP );
for ( j = 0 ; j < C - 1 ; j ++ )
{
fscanf ( f , "%f," , & m [ index ++ ]);
}
fscanf ( f , "%f" , & m [ index ++ ]);
while ( ! readUtl ( f , '\n' ) && i < R );
}
}
void saveMtx ( FILE * f , float * m , char * la )
{
int i ( 0 ), j ( 0 );
for ( i = 0 ; i < R ; i ++ )
{
fprintf ( f , "%c," , la [ i ]);
for ( j = 0 ; j < C - 1 ; j ++ )
{
fprintf ( f , "%.4f," , m [ i * C + j ]);
}
fprintf ( f , "%.4f" , m [ i * C + j ]);
fprintf ( f , " \n " );
}
}
编译运行:
1
./PCA wdbc.data wdbc.out 569 30
本文所采用的实验数据为开源数据集 ,该数据集是有关于乳腺癌诊断的相关数据,共有569条记录,每一个记录有30个特征,并且每一条记录都有一个标签,标签为’B’意味着良性,‘M’意味着恶性。上述代码对该数据集继续主成分分析,最后将输出矩阵保存在wdbc.out中。
下面我通过散点图的方式直观的展示分析的效果:
PCA一维映射
其中绿色代表良性,红色代表恶性。从图中可以看出,即使仅映射到一维,不同类别的数据似乎就已经很容易分离开了,这是因为我们选取的这个一维空间正是最大的那个特征值对应的空间,所以包含最多的信息。接下来我们将数据映射到二维和三维空间:
PCA二维映射
PCA三维映射
参考文献
[1]http://blog.codinglabs.org/articles/pca-tutorial.html
[2]https://blog.csdn.net/a10767891/article/details/80288463
[3]https://blog.csdn.net/itplus/article/details/11452743#commentsedit
[4]https://blog.csdn.net/daaikuaichuan/article/details/80620518
[5]https://blog.csdn.net/itplus/article/details/11451327
[6]http://setosa.io/ev/principal-component-analysis/